9647. Оптимальное умножение матриц
Имея две
матрицы A и B, мы можем вычислить C = AB, используя стандартные правила
умножения матриц:
![]()
Число
колонок в матрице A должно совпадать с числом строк матрицы B. Пусть матрица A
имеет размер m × n, матрица B имеет размер n × p. Тогда матрица С будет иметь
размер m × p, а для ее вычисления следует совершить m * n * p умножений.

Например,
если A имеет размер 10 × 20, B имеет размер 20 × 15, то необходимо
совершить 10 × 20 × 15 = 3000 умножений для вычисления матрицы C.
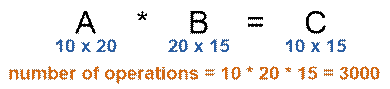
Перемножать
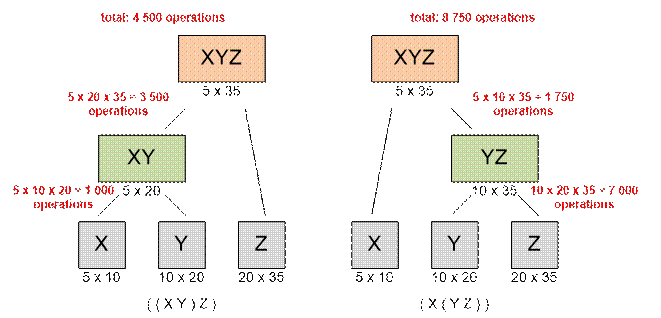
несколько матриц можно несколькими способами. Например, если у нас имеются
матрицы X, Y и Z, то вычислить XYZ можно либо как (XY)Z, либо как X(YZ). Пусть
X имеет размер 5 × 10, Y имеет
размер 10 × 20, Z имеет размер 20 × 35.

Подсчитаем
количество умножений, необходимых для перемножения трех матриц в каждом из этих
двух случаях:
(XY)Z
·
5 × 10 × 20 = 1000 умножений для определения матрицы (XY),
имеющей размер 5 × 20.
·
Потом 5 × 20 × 35 = 3500
умножений для нахождения конечного результата.
·
Общее количество умножений: 4500.
X(YZ)
·
10 × 20 × 35 = 7000 умножений для определения матрицы (YZ), имеющей
размер 10 × 35.
·
Потом 5 × 10 × 35 = 1750 умножений
для нахождения конечного результата.
·
Общее количество умножений: 8750.
Очевидно,
что при вычислении (XY)Z требуется меньшее количество умножений.
По
заданной последовательности перемножаемых матриц следует найти оптимальный
порядок их умножения. Оптимальным называется такой порядок умножения матриц,
при котором количество элементарных умножений минимально.
Вход. Первая строка содержит количество n (n ≤ 10) перемножаемых матриц. Далее следуют n пар целых чисел, описывающих количество строк и столбцов в матрице,
размеры матриц задаются в порядке их перемножения.
Выход. Выведите минимальное
количество умножений, достаточное для перемножения всех матриц.
|
Пример выхода 1 |
|
|
3 5 10 10 20 20 35 |
4500 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
6 30 35 35 15 15 5 5 10 10 20 20 25 |
15125 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Обозначим через Aij
произведение матриц Ai * Ai+1 *
… * Aj-1 * Aj (1 £ i £ j £ n). Пусть m[i, j]
– минимальное количество умножений, необходимое для вычисления Aij.
Стоимость вычисления всего произведения A1n будет храниться в
m[1, n]. Значения m[i, i] = 0, поскольку Aii
= Ai, и для его вычисления операции не требуются.
Количество столбцов матрицы Ai
равно количеству строк матрицы Ai+1. Это значение
хранится в p[i]. Количество строк матрицы А1 находится в
p[0], а количество столбцов матрицы An – в p[n].
Предположим, что при оптимальной
расстановке скобок в произведении Ai * … * Aj
последней операцией умножения будет
(Ai * … * Ak
) * (Ak+1
* … * Aj)
Значение m[i, j] равно
сумме минимальной стоимости вычислений Aik и Ak+1j
плюс стоимость умножения этих двух матриц:
m[i, j] = m[i, k]
+ m[k + 1, j] + p[i – 1] * p[k] * p[j]
При этом число k может
принимать только j – i разных значений: i, i + 1,
…, j – 1. Поскольку только одно из них является оптимальным, то
необходимо перебрать все эти значения и выбрать наилучшее. В результате
получаем рекуррентную формулу:
m[i, j] = 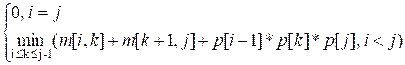
Для запоминания оптимального порядка умножения
положим s[i, j] = k, если при оптимальном вычислении Ai
* … * Aj последней операцией будет умножение Ai
* … * Ak на Ak+1 * … * Aj.
Пример
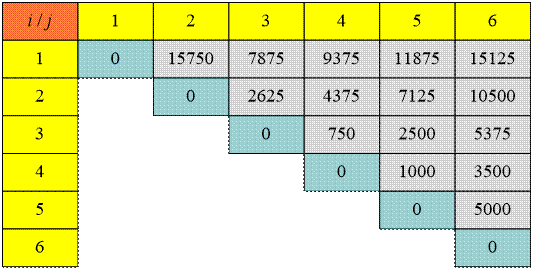
Рассмотрим
второй тест. Данные о размерах входных матриц сохраняются в массиве p:

Минимальная стоимость вычисления
матриц Aij хранится в ячейках массива m[i, j]:
Соответствующие
значения матрицы s:
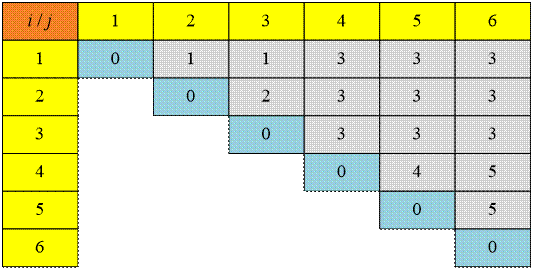
Для
умножения шести входных матриц достаточно выполнить m[1,6] = 15125
операций умножения. Оптимальная
последовательность умножений имеет вид:
A16
= (s[1,6] = 3) = A13 * A46 =
(s[1,3] =
1, s[4,6] = 5) = (A11 * A23) * (A45 * A66)
=
(s[2,3] =
2, s[4,5] = 4) = (A11 * (A22 * A33 ) ) * ((A44
* A55) * A66) =
(A1
* (A2 * A3 ) ) * ((A4 * A5) * A6)
Реализация алгоритма
Определим константы INF = ∞,
MAX = 11 (максимальное возможное количество матриц в произведении). Объявим
массивы dp и p.
#define INF 0x3F3F3F3F3F3F3F3F
#define MAX 11
long long dp[MAX][MAX], p[MAX];
Функция Mult возвращает
минимальное количество умножений, необходимое для вычисления Aij
= Ai * Ai+1 * … * Aj-1
* Aj, которое сохраняем в ячейке dp[i][ j].
long long Mult(int i, int j)
{
if (dp[i][j] == INF)
for (int k = i; k < j; k++)
dp[i][j] = min(dp[i][j], Mult(i, k) + Mult(k +
1, j) +
p[i - 1] * p[k] * p[j]);
return dp[i][j];
}
Основной цикл программы. Читаем количество матриц n.
scanf("%d",&n);
Присвоим всем ячейкам массива dp значение бесконечность (∞).
memset(dp,0x3F,sizeof(dp));
Читаем размеры входных матриц,
сохраняем их в массиве p. Положим dp[i][i] = 0.
for(i = 1; i <= n; i++)
{
scanf("%lld %lld",&p[i-1],&p[i]);
dp[i][i] = 0;
}
Вычисляем результат – ищем
оптимальное произведение матриц A1 * A2 * … * An-1
* An.
Mult(1,n);
Выводим ответ, который находится в ячейке dp[1][n].
printf("%lld", dp[1][n]);